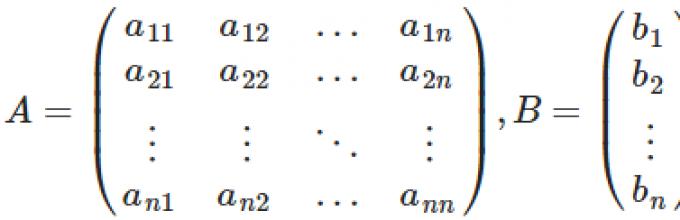Матричный метод решения СЛАУ применяют к решению систем уравнений, у которых количество уравнений соответствует количеству неизвестных. Метод лучше применять для решения систем низкого порядка. Матричный метод решения систем линейных уравнений основывается на применении свойств умножения матриц.
Этот способ, другими словами метод обратной матрицы, называют так, так как решение сводится к обычному матричному уравнению, для решения которого нужно найти обратную матрицу.
Матричный метод решения СЛАУ с определителем, который больше или меньше нуля состоит в следующем:
Предположим, есть СЛУ (система линейных уравнений) с n неизвестными (над произвольным полем):
Значит, её легко перевести в матричную форму:
AX=B , где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:
Умножим это матричное уравнение слева на A −1 — обратную матрицу к матрице A: A −1 (AX)=A −1 B.
Т.к. A −1 A=E , значит, X=A −1 B . Правая часть уравнения дает столбец решений начальной системы. Условием применимости матричного метода есть невырожденность матрицы A . Необходимым и достаточным условием этого есть неравенство нулю определителя матрицы A :
detA≠0.
Для однородной системы линейных уравнений , т.е. если вектор B=0 , выполняется обратное правило: у системы AX=0 есть нетривиальное (т.е. не равное нулю) решение лишь когда detA=0 . Эта связь между решениями однородных и неоднородных систем линейных уравнений называется альтернатива Фредгольма.
Т.о., решение СЛАУ матричным методом производится по формуле 
. Либо, решение СЛАУ находят при помощи обратной матрицы
A −1
.
Известно, что у квадратной матрицы А порядка n на n есть обратная матрица A −1 только в том случае, если ее определитель ненулевой. Таким образом, систему n линейных алгебраических уравнений с n неизвестными решаем матричным методом только в случае, если определитель основной матрицы системы не равен нулю.
Не взирая на то, что есть ограничения возможности применения такого метода и существуют сложности вычислений при больших значениях коэффициентов и систем высокого порядка, метод можно легко реализовать на ЭВМ.
Пример решения неоднородной СЛАУ.
Для начала проверим, не равен ли нулю определитель матрицы коэффициентов у неизвестных СЛАУ.
Теперь находим союзную матрицу , транспонируем её и подставляем в формулу для определения обратной матрицы.
Подставляем переменные в формулу:
Теперь находим неизвестные, перемножая обратную матрицу и столбик свободных членов.
Итак, x=2; y=1; z=4.
При переходе от обычного вида СЛАУ к матричной форме будьте внимательными с порядком неизвестных переменных в уравнениях системы. Например :
НЕЛЬЗЯ записать как:
Необходимо, для начала, упорядочить неизвестные переменные в кадом уравнении системы и только после этого переходить к матричной записи:
Кроме того, нужно быть внимательными с обозначением неизвестных переменных, вместо x 1 , x 2 , …, x n могут оказаться другие буквы. К примеру :
в матричной форме записываем так:
Матричным методом лучше решать системы линейных уравнений, в которых количество уравнений совпадает с числом неизвестных переменных и определитель основной матрицы системы не равен нулю. Когда в системе более 3-х уравнений, на нахождение обратной матрицы потребуется больше вычислительных усилий, поэтому, в этом случае целесообразно использовать для решения метод Гаусса.
Уравнения вообще, линейные алгебраические уравнения и их системы, а также методы их решения занимают в математике, как теоретической, так и прикладной, особое место.
Это связано с тем обстоятельством, что подавляющее большинство физических, экономических, технических и даже педагогических задач могут быть описаны и решены с помощью разнообразных уравнений и их систем. В последнее время особую популярность среди исследователей, ученых и практиков приобрело математическое моделирование практически во всех предметных областях, что объясняется очевидными его преимуществами перед другими известными и апробированными методами исследования объектов различной природы, в частности, так называемых, сложных систем. Существует великое многообразие различных определений математической модели, данных учеными в разные времена, но на наш взгляд, самое удачное, это следующее утверждение. Математическая модель – это идея, выраженная уравнением. Таким образом, умение составлять и решать уравнения и их системы – неотъемлемая характеристика современного специалиста.
Для решения систем линейных алгебраических уравнений наиболее часто используются методы: Крамера, Жордана-Гаусса и матричный метод.
Матричный метод решения - метод решения с помощью обратной матрицы систем линейных алгебраических уравнений с ненулевым определителем.
Если выписать коэффициенты при неизвестных величинах xi в матрицу A, неизвестные величины собрать в вектор столбец X, а свободные члены в вектор столбец B, то систему линейных алгебраических уравнений можно записать в виде следующего матричного уравнения A · X = B, которое имеет единственное решение только тогда, когда определитель матрицы A не будет равен нулю. При этом решение системы уравнений можно найти следующим способом X = A -1 · B , где A -1 - обратная матрица.
Матричный метод решения состоит в следующем.
Пусть дана система линейных уравнений с n неизвестными:
Её можно переписать в матричной форме: AX = B , где A - основная матрица системы, B и X - столбцы свободных членов и решений системы соответственно:
Умножим это матричное уравнение слева на A -1 - матрицу, обратную к матрице A : A -1 (AX ) = A -1 B
Так как A -1 A = E , получаем X = A -1 B . Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A . Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A : detA ≠ 0.
Для однородной системы линейных уравнений, то есть когда вектор B = 0 , действительно обратное правило: система AX = 0 имеет нетривиальное (то есть не нулевое) решение только если detA = 0. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.
Пример решения неоднородной системы линейных алгебраических уравнений .
Убедимся в том, что определитель матрицы, составленный из коэффициентов при неизвестных системы линейных алгебраических уравнений не равен нулю.
Следующим шагом будет вычисление алгебраических дополнений для элементов матрицы, состоящей из коэффициентов при неизвестных. Они понадобятся для нахождения обратной матрицы.
В данной статье мы расскажем о матричном методе решения системы линейных алгебраических уравнений, найдем его определение и приведем примеры решения.
Определение 1
Метод обратной матрицы - это метод, использующийся при решении СЛАУ в том случае, если число неизвестных равняется числу уравнений.
Пример 1
Найти решение системы n линейных уравнений с n неизвестными:
a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a n 1 x 1 + a n 2 x 2 + . . . + a n n x n = b n
Матричный вид записи : А × X = B
где А = а 11 а 12 ⋯ а 1 n а 21 а 22 ⋯ а 2 n ⋯ ⋯ ⋯ ⋯ а n 1 а n 2 ⋯ а n n - матрица системы.
X = x 1 x 2 ⋮ x n - столбец неизвестных,
B = b 1 b 2 ⋮ b n - столбец свободных коэффициентов.
Из уравнения, которое мы получили, необходимо выразить X . Для этого нужно умножить обе части матричного уравнения слева на A - 1:
A - 1 × A × X = A - 1 × B .
Так как А - 1 × А = Е, то Е × X = А - 1 × В или X = А - 1 × В.
Замечание
Обратная матрица к матрице А имеет право на существование только, если выполняется условие d e t A н е р а в е н н у л ю. Поэтому при решении СЛАУ методом обратной матрицы, в первую очередь находится d e t А.
В том случае, если d e t A н е р а в е н н у л ю, у системы имеется только один вариант решения: при помощи метода обратной матрицы. Если d e t А = 0 , то систему нельзя решить данным методом.
Пример решения системы линейных уравнений с помощью метода обратной матрицы
Пример 2Решаем СЛАУ методом обратной матрицы:
2 x 1 - 4 x 2 + 3 x 3 = 1 x 1 - 2 x 2 + 4 x 3 = 3 3 x 1 - x 2 + 5 x 3 = 2
Как решить?
- Записываем систему в виде матричного уравнения А X = B , где
А = 2 - 4 3 1 - 2 4 3 - 1 5 , X = x 1 x 2 x 3 , B = 1 3 2 .
- Выражаем из этого уравнения X:
- Находим определитель матрицы А:
d e t A = 2 - 4 3 1 - 2 4 3 - 1 5 = 2 × (- 2) × 5 + 3 × (- 4) × 4 + 3 × (- 1) × 1 - 3 × (- 2) × 3 - - 1 × (- 4) × 5 - 2 × 4 - (- 1) = - 20 - 48 - 3 + 18 + 20 + 8 = - 25
d e t А не равняется 0, следовательно для этой системы подходит метод решения обратной матрицей.
- Находим обратную матрицу А - 1 при помощи союзной матрицы. Вычисляем алгебраические дополнения А i j к соответствующим элементам матрицы А:
А 11 = (- 1) (1 + 1) - 2 4 - 1 5 = - 10 + 4 = - 6 ,
А 12 = (- 1) 1 + 2 1 4 3 5 = - (5 - 12) = 7 ,
А 13 = (- 1) 1 + 3 1 - 2 3 - 1 = - 1 + 6 = 5 ,
А 21 = (- 1) 2 + 1 - 4 3 - 1 5 = - (- 20 + 3) = 17 ,
А 22 = (- 1) 2 + 2 2 3 3 5 - 10 - 9 = 1 ,
А 23 = (- 1) 2 + 3 2 - 4 3 - 1 = - (- 2 + 12) = - 10 ,
А 31 = (- 1) 3 + 1 - 4 3 - 2 4 = - 16 + 6 = - 10 ,
А 32 = (- 1) 3 + 2 2 3 1 4 = - (8 - 3) = - 5 ,
А 33 = (- 1) 3 + 3 2 - 4 1 - 2 = - 4 + 4 = 0 .
- Записываем союзную матрицу А * , которая составлена из алгебраических дополнений матрицы А:
А * = - 6 7 5 17 1 - 10 - 10 - 5 0
- Записываем обратную матрицу согласно формуле:
A - 1 = 1 d e t A (A *) T: А - 1 = - 1 25 - 6 17 - 10 7 1 - 5 5 - 10 0 ,
- Умножаем обратную матрицу А - 1 на столбец свободных членов В и получаем решение системы:
X = A - 1 × B = - 1 25 - 6 17 - 10 7 1 - 5 5 - 10 0 1 3 2 = - 1 25 - 6 + 51 - 20 7 + 3 - 10 5 - 30 + 0 = - 1 0 1
Ответ : x 1 = - 1 ; x 2 = 0 ; x 3 = 1
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Назначение сервиса . С помощью данного онлайн-калькулятора вычисляются неизвестные {x 1 , x 2 , ..., x n } в системе уравнений. Решение осуществляется методом обратной матрицы . При этом:- вычисляется определитель матрицы A ;
- через алгебраические дополнения находится обратная матрица A -1 ;
- осуществляется создание шаблона решения в Excel ;
Инструкция . Для получения решения методом обратной матрицы необходимо задать размерность матрицы. Далее в новом диалоговом окне заполнить матрицу A и вектор результатов B .
Напомним, что решением системы линейных уравнений называется всякая совокупность чисел {x 1 , x 2 , ..., x n } , подстановка которых в эту систему вместо соответствующих неизвестных обращает каждое уравнение системы в тождество.
Система линейных алгебраических уравнений обычно записывается как (для 3-х переменных):
См. также Решение матричных уравнений .
Алгоритм решения
- Вычисляется определитель матрицы A . Если определитель равен нулю, то конец решения. Система имеет бесконечное множество решений.
- При определителе отличном от нуля, через алгебраические дополнения находится обратная матрица A -1 .
- Вектор решения X ={x 1 , x 2 , ..., x n } получается умножением обратной матрицы на вектор результата B .
Пример №1 . Найти решение системы матричным методом. Запишем матрицу в виде:
Алгебраические дополнения.
| A 1,1 = (-1) 1+1 |
| ∆ 1,1 = (1 (-2)-0 2) = -2 |
| A 1,2 = (-1) 1+2 |
| ∆ 1,2 = -(3 (-2)-1 2) = 8 |
| A 1,3 = (-1) 1+3 |
| ∆ 1,3 = (3 0-1 1) = -1 |
| A 2,1 = (-1) 2+1 |
| ∆ 2,1 = -(-2 (-2)-0 1) = -4 |
| A 2,2 = (-1) 2+2 |
| ∆ 2,2 = (2 (-2)-1 1) = -5 |
| A 2,3 = (-1) 2+3 |
| ∆ 2,3 = -(2 0-1 (-2)) = -2 |
| A 3,1 = (-1) 3+1 |
| ∆ 3,1 = (-2 2-1 1) = -5 |
| A 3,2 = (-1) 3+2 |
| ∆ 3,2 = -(2 2-3 1) = -1 |
| 3 |
| -2 |
| -1 |
X T = (1,0,1)
x 1 = -21 / -21 = 1
x 2 = 0 / -21 = 0
x 3 = -21 / -21 = 1
Проверка:
2 1+3 0+1 1 = 3
-2 1+1 0+0 1 = -2
1 1+2 0+-2 1 = -1
Пример №2
. Решить СЛАУ методом обратной матрицы.
2 x 1 + 3x 2 + 3x 3 + x 4 = 1
3 x 1 + 5x 2 + 3x 3 + 2x 4 = 2
5 x 1 + 7x 2 + 6x 3 + 2x 4 = 3
4 x 1 + 4x 2 + 3x 3 + x 4 = 4
Запишем матрицу в виде:
Вектор B:
B T = (1,2,3,4)
Главный определитель
Минор для (1,1):
= 5 (6 1-3 2)-7 (3 1-3 2)+4 (3 2-6 2) = -3
Минор для (2,1):
= 3 (6 1-3 2)-7 (3 1-3 1)+4 (3 2-6 1) = 0
Минор для (3,1):
= 3 (3 1-3 2)-5 (3 1-3 1)+4 (3 2-3 1) = 3
Минор для (4,1):
= 3 (3 2-6 2)-5 (3 2-6 1)+7 (3 2-3 1) = 3
Определитель минора
∆ = 2 (-3)-3 0+5 3-4 3 = -3
Пример №4
. Записать систему уравнений в матричной форме и решить с помощью обратной матрицы.
Решение :xls
Пример №5
. Дана система трех линейных уравнений с тремя неизвестными. Требуется: 1) найти ее решение с помощью формул Крамера ; 2) записать систему в матричной форме и решить ее средствами матричного исчисления.
Методические рекомендации
. После решения методом Крамера, найдите кнопку "Решение методом обратной матрицы для исходных данных". Вы получите соответствующее решение. Таким образом, данные вновь заполнять не придется.
Решение
. Обозначим через А - матрицу коэффициентов при неизвестных; X - матрицу-столбец неизвестных; B - матрицу-столбец свободных членов:
|
B T =(4,-3,-3)
С учетом этих обозначений данная система уравнений принимает следующую матричную форму: А*Х = B.
Если матрица А - невырожденная (ее определитель отличен от нуля, то она имеет обратную матрицу А -1 . Умножив обе части уравнения на А -1 , получим: А -1 *А*Х = А -1 *B, А -1 *А=Е.
Это равенство называется матричной записью решения системы линейных уравнений . Для нахождения решения системы уравнений необходимо вычислить обратную матрицу А -1 .
Система будет иметь решение, если определитель матрицы A отличен от нуля.
Найдем главный определитель.
∆=-1 (-2 (-1)-1 1)-3 (3 (-1)-1 0)+2 (3 1-(-2 0))=14
Итак, определитель 14 ≠ 0, поэтому продолжаем решение. Для этого найдем обратную матрицу через алгебраические дополнения.
Пусть имеем невырожденную матрицу А:
| A 1,1 =(-1) 1+1 |
|
| A 1,2 =(-1) 1+2 |
|
| A 1,3 =(-1) 1+3 |
|
| A 2,1 =(-1) 2+1 |
|
| A 2,2 =(-1) 2+2 |
|
| A 2,3 =(-1) 2+3 |
|
| A 3,1 =(-1) 3+1 |
|
| 4 |
| -3 |
| -3 |
| X=1/14 |
|
∆=4 (0 1-3 (-2))-2 (1 1-3 (-1))+0 (1 (-2)-0 (-1))=16
Транспонированная матрица
| A 1,2 =(-1) 1+2 |
|
| A 1,3 =(-1) 1+3 |
|
| A 2,1 =(-1) 2+1 |
|
| A 2,2 =(-1) 2+2 |
|
| A 2,3 =(-1) 2+3 |
|
| A 3,1 =(-1) 3+1 |
|
| A 3,2 =(-1) 3+2 |
|
| A 3,3 =(-1) 3+3 | 1/16 |
|
| (4 6)+(1 (-2))+(-1 6) | (4 (-4))+(1 4)+(-1 (-12)) | (4 (-2))+(1 6)+(-1 (-2)) |
| (2 6)+(0 (-2))+(-2 6) | (2 (-4))+(0 4)+(-2 (-12)) | (2 (-2))+(0 6)+(-2 (-2)) |
| (0 6)+(3 (-2))+(1 6) | (0 (-4))+(3 4)+(1 (-12)) | (0 (-2))+(3 6)+(1 (-2)) |
| =1/16 |
|
| A*A -1 = |
|
Пример №7
. Решение матричных уравнений.
Обозначим:
| A = |
|
| A 1,1 = (-1) 1+1 |
|
| A 1,2 = (-1) 1+2 |
|
| A 1,3 = (-1) 1+3 |
|
| A 2,1 = (-1) 2+1 |
|
| A 2,2 = (-1) 2+2 |
|
| A 2,3 = (-1) 2+3 |
|
| A 3,1 = (-1) 3+1 |
|
| -12 | 15 | -5 |
| -4 | 5 | -2 |
| 7 | -9 | 3 |
B T =(31,13,10)
X T =(4.05,6.13,7.54)
x 1 = 158 / 39 =4.05
x 2 = 239 / 39 =6.13
x 3 = 294 / 39 =7.54
Проверка
.
-2 4.05+-1 6.13+6 7.54=31
1 4.05+-1 6.13+2 7.54=13
2 4.05+4 6.13+-3 7.54=10
Пример №9
. Обозначим через А - матрицу коэффициентов при неизвестных; X - матрицу-столбец неизвестных; B - матрицу-столбец свободных членов:
|
B T =(31,13,10)
X T =(5.21,4.51,6.15)
x 1 = 276 / 53 =5.21
x 2 = 239 / 53 =4.51
x 3 = 326 / 53 =6.15
Проверка
.
-2 5.21+1 4.51+6 6.15=31
1 5.21+-1 4.51+2 6.15=13
2 5.21+4 4.51+-3 6.15=10
Пример №10
. Решение матричных уравнений.
Обозначим:
A 11 = (-1) 1+1 ·-3 = -3; A 12 = (-1) 1+2 ·3 = -3; A 21 = (-1) 2+1 ·1 = -1; A 22 = (-1) 2+2 ·2 = 2;
Обратная матрица A -1 .
| -3 | -3 |
| -1 | 2 |
| 1 | -2 |
| 1 | 1 |
| X = |
|
Решение систем линейных алгебраических уравнений матричным методом (с помощью обратной матрицы).
Пусть система линейных алгебраических уравнений задана в матричной форме , где матрицаA имеет размерностьn наn и ее определитель отличен от нуля.
Так как , то матрицаА – обратима, то есть, существует обратная матрица. Если умножить обе части равенстванаслева, то получим формулу для нахождения матрицы-столбца неизвестных переменных. Так мы получили решение системы линейных алгебраических уравнений матричным методом.
матричным
методом.
Перепишем
систему уравнений в матричной форме:
Так
как
то
СЛАУ можно решать матричным методом. С
помощью обратной матрицы решение этой
системы может быть найдено как
.
Построим
обратную матрицу
с
помощью матрицы из алгебраических
дополнений элементов матрицыА
(при
необходимости смотрите статьюметоды
нахождения обратной матрицы):
Осталось
вычислить
-
матрицу неизвестных переменных, умножив
обратную матрицу
на
матрицу-столбец свободных членов(при
необходимости смотрите статьюоперации
над матрицами):
или
в другой записи x
1
= 4, x
2
= 0, x
3
= -1
.
Основная проблема при нахождении решения систем линейных алгебраических уравнений матричным методом заключается в трудоемкости нахождения обратной матрицы, особенно для квадратных матриц порядка выше третьего.
Более подробное описание теории и дополнительные примеры смотрите в статье матричный метод решения систем линейных уравнений.
К началу страницы
Решение систем линейных уравнений методом Гаусса.
Пусть
нам требуется найти решение системы из
n
линейных уравнений сn
неизвестными
переменными
определитель
основной матрицы которой отличен от
нуля.
Суть метода Гаусса состоит в последовательном исключении неизвестных переменных: сначала исключаетсяx 1 из всех уравнений системы, начиная со второго, далее исключаетсяx 2 из всех уравнений, начиная с третьего, и так далее, пока в последнем уравнении останется только неизвестная переменнаяx n . Такой процесс преобразования уравнений системы для последовательного исключения неизвестных переменных называетсяпрямым ходом метода Гаусса . После завершения прямого хода метода Гаусса из последнего уравнения находитсяx n , с помощью этого значения из предпоследнего уравнения вычисляетсяx n-1 , и так далее, из первого уравнения находитсяx 1 . Процесс вычисления неизвестных переменных при движении от последнего уравнения системы к первому называетсяобратным ходом метода Гаусса .
Кратко опишем алгоритм исключения неизвестных переменных.
Будем
считать, что
,
так как мы всегда можем этого добиться
перестановкой местами уравнений системы.
Исключим неизвестную переменнуюx
1
из всех уравнений системы, начиная со
второго. Для этого ко второму уравнению
системы прибавим первое, умноженное на,
к третьему уравнению прибавим первое,
умноженное на,
и так далее, кn-ому
уравнению прибавим
первое, умноженное на.
Система уравнений после таких
преобразований примет вид
где,
а
.
К такому же результату мы бы пришли, если бы выразили x 1 через другие неизвестные переменные в первом уравнении системы и полученное выражение подставили во все остальные уравнения. Таким образом, переменнаяx 1 исключена из всех уравнений, начиная со второго.
Далее
действуем аналогично, но лишь с частью
полученной системы, которая отмечена
на рисунке
Для
этого к третьему уравнению системы
прибавим второе, умноженное на
,
к четвертому уравнению прибавим второе,
умноженное на,
и так далее, кn-ому
уравнению прибавим
второе, умноженное на.
Система уравнений после таких
преобразований примет вид
где,
а
.
Таким образом, переменнаяx
2
исключена из всех уравнений, начиная с
третьего.
Далее
приступаем к исключению неизвестной
x
3
, при этом действуем
аналогично с отмеченной на рисунке
частью системы
Так
продолжаем прямой ход метода Гаусса
пока система не примет вид
С этого момента начинаем обратный ход метода Гаусса: вычисляем x n из последнего уравнения как, с помощью полученного значенияx n находимx n-1 из предпоследнего уравнения, и так далее, находимx 1 из первого уравнения.
Решите
систему линейных уравнений
методом
Гаусса.
Исключим
неизвестную переменную x
1
из второго и третьего уравнения системы.
Для этого к обеим частям второго и
третьего уравнений прибавим соответствующие
части первого уравнения, умноженные наи
насоответственно:
Теперь
из третьего уравнения исключим x
2
,
прибавив к его левой и правой частям
левую и правую части второго уравнения,
умноженные на:
На этом прямой ход метода Гаусса закончен, начинаем обратный ход.
Из
последнего уравнения полученной системы
уравнений находим x
3
:
Из второго уравнения получаем .
Из первого уравнения находим оставшуюся неизвестную переменную и этим завершаем обратный ход метода Гаусса .
x 1 = 4, x 2 = 0, x 3 = -1 .
Более детальную информацию и дополнительные примеры смотрите в разделе решение элементарных систем линейных алгебраических уравнений методом Гаусса.
К началу страницы
