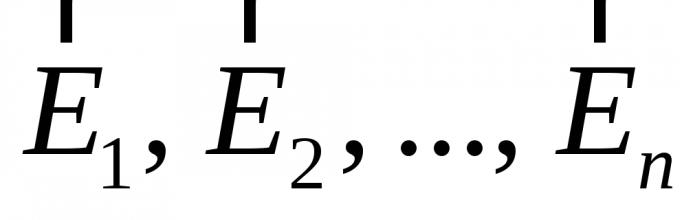Напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряженностей электрических полей, создаваемых в той же точке зарядами в отдельности:
→ n → → →
Е = Σ Еi = Е 1 + Е 2 + …
Потенциал поля системы зарядов равен алгебраической сумме потенциалов в каждой точке по отдельности:
φ = Σ φi = φ 1 + φ 2 + …
Эти свойства электрического поля означает, что поле подчиняется принципу суперпозиции.
Теорема Гаусса и её применение для расчёта напряжённости электрического поля бесконечной равномерно заряженной плоскости, двух и более плоскостей; бесконечной равномерно заряженной нити, цилиндра; равномерно заряженной сферы, объёмно заряженного шара.
Теорема Гаусса : Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, поделенной на электрическую постоянную ε 0 .
Ф = ∫ Еп ds = 1/ ε 0 Σ qi
1.Поле равномерно заряженной бесконечной плоскости . Бесконечная плоскость (рис. 1) заряжена с постоянной поверхностной плотностью +σ (σ = dQ/dS - заряд, который приходится на единицу поверхности). Линии напряженности перпендикулярны данной плоскости и направлены от нее в каждую из сторон. Возьмем в качестве замкнутой поверхности цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллельны линиям напряженности поля (соsα=0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания (площади оснований равны и для основания Е n совпадает с Е), т. е. равен 2ES. Заряд, который заключен внутри построенной цилиндрической поверхности, равен σ∙S. Согласно теореме Гаусса, 2E∙S= σ ∙S/ε 0 , откуда
2.Поле двух бесконечных параллельных разноименно заряженных плоскостей (рис. 2). Пусть плоскости заряжены равномерно разными по знаку зарядами с поверхностными плотностями +σ и –σ. Поле таких плоскостей будем искать как суперпозицию полей, которые создаются каждой из плоскостей в отдельности. На рисунке верхние стрелки соответствуют полю от положительно заряженной плоскости, нижние - от отрицательно заряженной плоскости. Слева и справа от плоскостей поля вычитаются (поскольку линии напряженности направлены навстречу друг другу), значит здесь напряженность поля E=0. В области между плоскостями E = E+ + E- (E+ и E- находятся по формуле (1)), поэтому результирующая напряженность
3.Поле равномерно заряженного бесконечного цилиндра (нити) . Бесконечный цилиндр радиуса R (рис. 6) равномерно заряжен с линейной плотностью τ (τ = –dQ/dt заряд, который приходится на единицу длины). Из соображений симметрии мы видим, что линии напряженности будут направлены по радиусам круговых сечений цилиндра с одинаковой густотой во все стороны относительно оси цилиндра. Мысленно построим в качестве замкнутой поверхности коаксиальный цилиндр радиуса r и высотой l . Поток вектора Е сквозь торцы коаксиального цилиндра равен нулю (торцы и линии напряженности параллельны), а сквозь боковую поверхность равен 2πrl Е. Используя теорему Гаусса, при r>R 2πrl Е = τl /ε 0 , откуда
Если r 4.Поле равномерно заряженной сферической поверхности
. Сферическая поверхность радиуса R с общим зарядом Q заряжена равномерно с поверхностной плотностью
+σ. Т.к. заряд распределен равномерно по поверхности то поле, которое создается им, обладает сферической симметрией. Значит линии напряженности направлены радиально (рис. 3). Проведем мысленно сферу радиуса r, которая имеет общий центр с заряженной сферой. Если r>R,ro внутрь поверхности попадает весь заряд Q, который создает рассматриваемое поле, и, по теореме Гаусса, 4πr 2 E = Q/ε 0 , откуда При r>R поле убывает с расстоянием r по такому же закону, как у точечного заряда. График зависимости Е от r приведен на рис. 4. Если r" 5.Поле объемно заряженного шара
. Шар радиуса R с общим зарядом Q заряжен равномерно с объемной плотностью
ρ (ρ = dQ/dV – заряд, который приходится на единицу объема). Учитывая соображения симметрии, аналогичные п.3, можно доказать, что для напряженности поля вне шара получится тот же результат, что и в случае (3). Внутри же шара напряженность поля будет иная. Сфера радиуса r" Значит, напряженность поля вне равномерно заряженного шара описывается формулой (3), а внутри его изменяется линейно с расстоянием r" согласно зависимости (4). График зависимости Е от r для рассмотренного случая показан на рис. 5. Взаимодействие между зарядами осуществляется через электрическое поле. Электрическое поле покоящихся зарядов называется электростатическим. Электростатическое поле
- поле, созданное неподвижными в пространстве и неизменными во времени электрическими зарядами (при отсутствии электрических токов). Электрическое поле представляет собой особый вид материи, связанный с электрическими зарядами и передающий действия зарядов друг на друга. Электростатическое поле отдельного заряда можно обнаружить, если внести в это поле другой заряд, на который в соответствии с законом Кулона будет действовать определенная сила. Напряженность
поля есть векторная величина, численно равная силе, действующей на единичный положительный точечный заряд, помещенный в данную точку поля . [E]=Н/Кл=(м*кг)/(см3*A1)=В/м. Направление вектора напряженности совпадает с направлением действия силы. Определим напряженность поля, создаваемого точечным зарядом q на некотором расстоянии r от него в вакууме ; . Если в одну и туже точку помещать разные пробные заряды q1 , q2 и т.д., то на них будут действовать различные силы, пропорциональные этим зарядам. Отношение для всех зарядов, вносимых в поле, будет одинаковым и будет зависеть лишь от q и r, определяющих электрическое поле в данной точке. Напряженность данной точки электрического поля это сила действующая на единичный положительный заряд, помещенный в эту точку. За единицу напряженности принимается напряженность в такой точке поля, в которой на единицу заряда действует единица силы. Принцип суперпозиции полей.
Результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил. Принцип суперпозиции полей, или принцип наложения, является условностью, согласно которой некоторый сложный процесс взаимодействия между определённым числом объектов можно представить в виде суммы взаимодействий между отдельными объектами. Принцип суперпозиции применим лишь к тем системам, которые описываются линейными уравнениями. Графически принцип суперпозиции полей можно представить в виде геометрической суммы векторов силы, которые действуют на пробный заряд, помещённый в поле точечных электрических зарядов. Если поле создано простейшей совокупностью зарядов, которая состоит из положительного и отрицательного зарядов, находящихся на некотором расстоянии друг от друга, то результирующее поле в точке наблюдения находится с помощью правила параллелограмма. Нельзя применять принцип суперпозиции к взаимодействию атомов и молекул между собой. Например, если взять два атома, у которых электроны находятся во взаимодействии, и поднести к ним третий такой же атом. Часть электронов от первых двух атомов притянется и вступит во взаимодействие с третьим атомом. Т.е. первоначальное распределение энергии в системе изменится. Изначальная сила взаимодействия между электронами и ядрами первых двух атомов уменьшится. Т.е. третий атом влияет не только на электроны, но и на ядра атомов. Также принцип суперпозиции нельзя применять для нелинейный систем. Закон Кулона описывает электрическое
взаимодействие только двух покоящихся
зарядов. Как же найти силу, действующую
на некий заряд со стороны нескольких
других зарядов? Ответ на этот вопрос
дает принцип суперпозиции
электрических полей:Напряженность
электрического поля
,
созданного несколькими неподвижными
точечными зарядами
q
1
,
q
2
,...,
q
n
,
равна векторной сумме напряженностей
электрических полей
Другими словами, принцип суперпозиции
утверждает, что сила взаимодействия
двух точечных зарядов не зависит от
того, подвергаются эти заряды действию
других зарядов или нет. Рис.1.6. Электрическое поле системы
зарядов как суперпозиция полей отдельных
зарядов
Итак, для системы N
точечных зарядов
(рис.1.6) на основании принципа суперпозиции
результирующее поле определяется
выражением Напряженность электрического поля
созданного в точке наблюдения системой
зарядов равна векторной сумме
напряженностей электрических полей,
созданных в этой же точке наблюдения
отдельными зарядами упомянутой системы. Рис. поясняет принцип
суперпозиции на примере электростатического
взаимодействия трех заряженных тел. Здесь важны 2
момента: векторное сложение и независимость
поля каждого заряда от присутствия
других зарядов. Если это мы будем говорить
о достаточно точечных телах, о достаточно
небольших размерах, тогда суперпозиция
работает. Однако известно, что в достаточно
сильных электрических полях этот принцип
уже не работает. Часто дискретность распределения
электрических зарядов бывает несущественна
при расчете полей. При этом математические
расчеты существенно упрощаются, если
истинное распределение точечных зарядов
заменить фиктивным непрерывным
распределением. Если дискретные заряды распределены в
объеме, то при переходе к непрерывному
распределению вводят понятие объемной
плотности заряда по определению где dq
- заряд, сосредоточенный в
объемеdV
(рис.1.8,а). Рис.1.8. Выделение
элементарного заряда в случаях объемно
заряженной области (а); поверхностно
заряженной области (б); линейно заряженной
области (в)
Если дискретные
заряды расположены в тонком слое, то
вводят понятие поверхностной плотности
заряда по определению где dq
- заряд, приходящийся на элемент
поверхности dS
(рис.1.8,б). Если дискретные
заряды локализованы внутри тонкого
цилиндра, вводят понятие линейной
плотности заряда где dq
- заряд на элементе длины цилиндра dl
(рис.1.8,в). С использованием введенных
распределений выражение для электрического
поля в точке А
системы зарядов (1.5) запишется в виде Найти напряженность
О Случай полубесконечной
нити; Случай бесконечной
нити: Одна из задач, которые ставит электростатика перед собой – это оценка параметров поля при заданном стационарном распределении зарядов в пространстве. И принцип суперпозиции является одним из вариантов решения такой задачи. Предположим наличие трех точечных зарядов, находящихся во взаимодействии друг с другом. При помощи эксперимента возможно осуществить измерение сил, действующих на каждый из зарядов. Для нахождения суммарной силы, с которой на один заряд действуют два других заряда, нужно силы воздействия каждого из этих двух сложить по правилу параллелограмма. При этом логичен вопрос: равны ли друг другу измеряемая сила, которая действует на каждый из зарядов, и совокупность сил со стороны двух иных зарядов, если силы рассчитаны по закону Кулона. Результаты исследований демонстрируют положительный ответ на этот вопрос: действительно, измеряемая сила равна сумме вычисляемых сил согласно закону Кулона со стороны других зарядов. Данное заключение записывается в виде совокупности утверждений и носит название принципа суперпозиции. Определение 1
Принцип суперпозиции
: Принцип суперпозиции полей заряда является одним из фундаментов изучения такого явления, как электричество: значимость его сопоставима с важностью закона Кулона. В случае, когда речь идет о множестве зарядов N (т.е. нескольких источников поля), суммарную силу, которую испытывает на себе пробный заряд q
, можно определить по формуле: F → = ∑ i = 1 N F i a → , где F i a → является силой, с которой влияет на заряд q
заряд
q i , если прочий N - 1 заряд отсутствует. При помощи принципа суперпозиции с использованием закона взаимодействия между точечными зарядами существует возможность определить силу взаимодействия между зарядами, присутствующими на теле конечных размеров. С этой целью каждый заряд разбивается на малые заряды d q (будем считать их точечными), которые затем берутся попарно; вычисляется сила взаимодействия и в заключение осуществляется векторное сложение полученных сил. Полевая трактовка
: напряженность поля двух точечных зарядов есть сумма напряженностей, создаваемым каждым из зарядов при отсутствии другого. Для общих случаев принцип суперпозиции относительно напряженностей имеет следующую запись: E → = ∑ E i → , где E i → = 1 4 π ε 0 q i ε r i 3 r i → является напряженностью i -го точечного заряда, r i → - радиусом вектора, проложенного от i -го заряда в некоторую точку пространства. Указанная формула говорит нам о том, что напряженность поля любого числа точечных зарядов есть сумма напряженностей полей каждого из точечных зарядов, если другие отсутствуют. Инженерная практика подтверждает соблюдение принципа суперпозиции даже для очень больших напряженностей полей. Значимым размером напряженности обладают поля в атомах и ядрах (порядка 10 11 - 10 17 В м), но и в этом случае применялся принцип суперпозиции для расчетов энергетических уровней. При этом наблюдалось совпадение результатов расчетов с данными экспериментов с большой точностью. Все же следует также заметить, что в случае очень малых расстояний (порядка ~ 10 - 15 м) и экстремально сильных полей принцип суперпозиции, вероятно, не выполняется. Пример 1
Например, на поверхности тяжелых ядер при напряженности порядка ~ 10 22 В м принцип суперпозиции выполняется, а при напряженности 10 20 В м возникают квантово-механические нелинейности взаимодействия. Когда распределение заряда является непрерывным (т.е. отсутствует необходимость учета дискретности), совокупная напряженность поля задается формулой: E → = ∫ d E → . В этой записи интегрирование проводится по области распределения зарядов: Принцип суперпозиции дает возможность находить E → для любой точки пространства при известном типе пространственного распределения заряда. Заданы одинаковые точечные заряды q , расположенные в вершинах квадрата со стороной a . Необходимо определить, какая сила воздействует на каждый заряд со стороны других трех зарядов. Решение
На рисунке 1 проиллюстрируем силы, влияющие на любой из заданных зарядов в вершинах квадрата. Поскольку условием задано, что заряды одинаковы, для иллюстрации возможно выбрать любой из них. Сделаем запись суммирующей силы, влияющей на заряд q 1: F → = F 12 → + F 14 → + F 13 → . Силы F 12 → и F 14 → являются равными по модулю, определим их так: F 13 → = k q 2 2 a 2 . Рисунок
1 Теперь зададим направление оси О Х (рисунок 1), спроектируем уравнение F → = F 12 → + F 14 → + F 13 → , подставим в него полученные выше модули сил и тогда: F = 2 k q 2 a 2 · 2 2 + k q 2 2 a 2 = k q 2 a 2 2 2 + 1 2 . Ответ:
сила, оказывающее воздействие на каждый из заданных зарядов, находящихся в вершинах квадрата, равна F = k q 2 a 2 2 2 + 1 2 . Пример 3
Задан электрический заряд, распределенный равномерно вдоль тонкой нити (с линейной плотностью τ). Необходимо записать выражение, определяющее напряженность поля на расстоянии a от конца нити вдоль ее продолжения. Длина нити – l .
Рисунок
2 Решение
Первым нашим шагом будет выделение на нити точечного заряда d q
. Составим для него, в соответствии с законом Кулона, запись, выражающую напряженность электростатического поля: d E → = k d q r 3 r → . В заданной точке все векторы напряженности имеют одинаковую направленность вдоль оси ОХ, тогда: d E x = k d q r 2 = d E . Условием задачи дано, что заряд имеет равномерное распределение вдоль нити с заданной плотностью, и запишем следующее: Подставим эту запись в записанное ранее выражение напряженности электростатического поля, проинтегрируем и получим: E = k ∫ a l + a τ d r r 2 = k τ - 1 r a l + a = k τ l a (l + a) . Ответ:
напряженность поля в указанной точке будет определяться по формуле E = k τ l a (l + a) . Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter Рассмотрим метод определения модуля и направления вектора напряженности Е в каждой точке электростатического поля, создаваемого системой неподвижных зарядов Q 1 , Q 2 ,
…,Q n .
Опыт показывает, что к кулоновским силам применим рассмотренный в механике принцип независимости действия сил (см. § 6), т. е. результирующая силаF,
действующая со стороны поля на пробный заряд Q 0
, равна векторной сумме сил F i
, приложенных к нему со стороны каждого из зарядов Qi:
Согласно (79.1), и , где Е-напряженность результирующего поля, а Еi
- напряженность поля, создаваемого зарядом Qi
;. Подставляя последние выражения в (80.1), получаем Формула (80.2) выражаетпринцип суперпозиции (наложения) электростатических полей,
согласно которому напряженность Е результирующего поля, создаваемого системой зарядов, равна геометрической сумме
напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности. Принцип суперпозиции применим для расчета электростатического поля электрического диполя.Электрический
диполь - система двух равных по модулю разно именных точечных зарядов (+Q,
-Q),
расстояние l
между которыми значительно меньше расстояния до рассматриваемых точек поля. Вектор, направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положительному и равный расстоянию между ними, называетсяплечом диполя 1.
Вектор совпадающий по направлению с плечом диполя и равный произведению заряда |Q
| на плечо l
, называетсяэлектрическим моментом диполя
илидипольным моментом
(рис. 122). Рис. 122
где Е+ и Е- - напряженности полей, создаваемых соответственно положительным и отрицательным зарядами. Воспользовавшись этой формулой, рассчитаем напряженность поля в произвольной точке на продолжении оси диполя и на перпендикуляре к середине его оси. 1. Напряженность поля на продолжении оси диполя
в точке А
(рис. 123). Как видно из рисунка, напряженность поля диполя в точке А
направлена по оси диполя и по модулю равна Рис.
123 Обозначив расстояние от точки А
до середины оси диполя через г, на основании формулы (79.2) для вакуума можно записать ,
которые создавал бы каждый из этих
зарядов в той же точке наблюдения в
отсутствие остальных:
,
которые создавал бы каждый из этих
зарядов в той же точке наблюдения в
отсутствие остальных:
 (1.5)
(1.5)
![]() .
.
![]()
![]()
![]()
1.7. Распределение зарядов
 ,
,


 ,
, ,
,


1.8. Примеры расчета электростатических полей в вакууме.
1.8.1. Полепрямолинейного отрезка нити (см. Орокс, примеры 1.9, 1.10) (Пример 1).
 электрического поля, созданного отрезком
тонкой, однородно заряженной с линейной
плотностью
электрического поля, созданного отрезком
тонкой, однородно заряженной с линейной
плотностью
 нити (см.рис).
Углы
1
,
2
и расстояние
r
известны.
нити (см.рис).
Углы
1
,
2
и расстояние
r
известны.
 трезок
разбивают на небольшие отрезки, каждый
из которых относительно точки наблюдения
можно считать точечным.
трезок
разбивают на небольшие отрезки, каждый
из которых относительно точки наблюдения
можно считать точечным.
 ;
;









Принцип суперпозиции
Полевая трактовка принципа суперпозиции
Определение 2

![]() (80.2)
(80.2)